Divide and Conquer

Imagine a classroom scenario where students are asked to organize a large number of books in a library. The problem of categorizing and shelving thousands of books can seem difficult at first. By applying divide-and-conquer principles, the task can be simplified significantly.The students can start by dividing the books into smaller groups based on genres, such as fiction, non-fiction, and reference. Each genre can then be further subdivided into categories like science fiction, historical novels,and biographies. Finally, within each category, the books can be organized alphabetically by author. This method of dividing the problem into manageable parts, solving each part, and then combining the results effectively demonstrates how divide-and-conquer can make complex tasks more approachable

In software development, the divide-and-conquer approach is frequently employed in designing complex systems and applications. For instance, consider developing a comprehensive e-commerce platform. The platform is divided into various functional modules, such as user authentication, product catalog, shopping cart, and payment processing. Each module is developed and tested independently, allowing developers to focus on specific aspects of the system. Once all modules are completed, they are integrated to form a cohesive application.This method ensures that the development process is manageable and that each component functions correctly before being combined into the final product.

Let's dive into the Divide and Conquer method, which is a powerful and fundamental problem-solving technique, especially in computer science and algorithm design.

What is Divide and Conquer?

Divide and Conquer is an algorithmic paradigm where a problem is broken down into smaller, more manageable sub-problems. Each of these sub-problems is solved independently, and their solutions are then combined to form the solution to the original problem. This approach is particularly effective for problems that can be recursively divided into similar sub-problems.

Steps in Divide and Conquer

The Divide and Conquer approach typically involves three steps:

Divide: The original problem is divided into smaller sub-problems. These sub-problems are generally smaller instances of the same type of problem. The division continues recursively until the sub-problems become simple enough to be solved directly.

        Consider the task of organizing a large set of files into a well-structured directory system. The first step involves breaking down this problem into smaller, more manageable subproblems. For instance, you might divide the files by their type (e.g., documents, images, videos) or by their project affiliation. Each subset of files is then considered a subproblem, which is more straightforward to organize than the entire set of files. The key is to ensure that each subset is similar to the original problem but simpler to handle individually.

Conquer: The smaller sub-problems are solved independently. If the sub-problem is small enough, it is solved directly (this is often referred to as the base case in recursion). Otherwise, the Divide and Conquer approach is applied recursively to solve the sub-problems.

Once the files are divided into smaller subsets, each subset is organized recursively. For example, you could sort documents into subcategories such as reports, presentations, and spreadsheets. Each of these categories might be further divided into subfolders based on date or project. This recursive approach allows you to systematically manage and categorize each subset. For very small subsets, such as a single folder with a few files, a direct solution is applied without further division, making the problem solving process more manageable.

Combine: The solutions to the sub-problems are combined to produce the solution to the original problem. This step often involves merging or assembling the partial solutions into a complete solution.

Example: Merge Sort

Let’s take the example of the Merge Sort algorithm to illustrate how Divide and Conquer works:

Step 1: Divide

• Problem: Sort an array of n elements.
• Divide: Split the array into two halves. If the array has n elements, you create two sub-arrays, each containing n/2 elements.

Step 2: Conquer

• Recursion: Recursively apply Merge Sort to each of the two sub-arrays.
• Base Case: If a sub-array has only one element, it is already sorted, so no further action is needed.

Step 3: Combine

• Merging: Merge the two sorted sub-arrays to form a single sorted array. This merging process involves comparing elements from both sub-arrays and arranging them in sorted order.

Example: Merge Sort Visualization

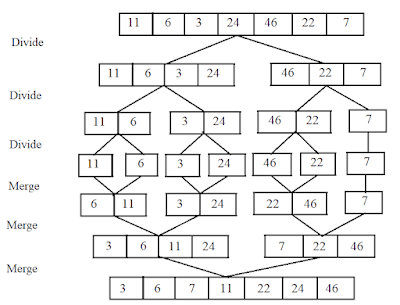
Here’s how Merge Sort would work on an array [11, 6, 3, 24, 46, 22, 7]:

1. Divide:

   • Split the array into [11, 6, 3, 24] and [46, 22, 7].
   • Further divide [[11, 6, 3, 24] into [11, 6] and [3,24], and [46, 22, 7] into [46,22] and [7].
   • Continue dividing until you have sub-arrays of single elements: [11], [6], [3], [24], [46], [22], [7].

2. Conquer:

   • Merge [11] and [6] to get [6, 11].
   • Merge [3] and [24] to get [3, 24].
   • Merge [46] and [22] to get [22,46].
   • Now, you have [6, 11], [3, 24], [22, 46],[7]

3. Combine:

   • Merge [6, 11] and [3, 24] to get [3, 6, 11, 24].
   • Merge [22,46] and [7] to get [7,22,46].
   • Finally, merge [3,6,11,24] and [7,22,46] to get the fully sorted array [3, 6, 7, 11, 22, 24,46].

Advantages of Divide and Conquer

1. Simplicity in Problem Solving: By breaking a problem into smaller sub problems, each sub problem is simpler to understand and solve, making the overall problem more manageable.

2. Efficiency: Many divide-and-conquer algorithms, such as merge sort and quicksort, have optimal or near-optimal time complexities. These algorithms often have lower time complexities compared to iterative approaches.

3. Modularity: Divide-and-conquer promotes a modular approach to problemsolving, where each subproblem can be handled by a separate function or module. This makes the code easier to maintain and extend.

4. Reduction in Complexity: By dividing the problem, the overall complexity is reduced, and solving smaller subproblems can lead to simpler and more efficient solutions.

5. Parallelism: The divide-and-conquer approach can easily be parallelized because the subproblems can be solved independently and simultaneously on different processors, leading to potential performance improvements.

6. Better Use of Memory: Some divide-and-conquer algorithms use memory more efficiently. For example, the merge sort algorithm works well with large data sets that do not fit into memory, as it can process subsets of data in chunks.

Disadvantages of Divide and Conquer

1. Overhead of Recursive Calls: The recursive nature can lead to significant overhead due to function calls and maintaining the call stack. This can be a problem for algorithms with deep recursion or large subproblem sizes.

2. Increased Memory Usage: Divide-and-conquer algorithms often require additional memory for storing intermediate results, which can be a drawback for memory-constrained environments.

3. Complexity of Merging Results: The merging step can be complex and may not always be straightforward. Efficient merging often requires additional algorithms and can add to the complexity of the overall solution. This difficulty in combining solutions can make the implementation of Divide and Conquer algorithms more challenging, especially for problems where the interaction between sub problems is intricate.

4. Not Always the Most Efficient: For some problems, divide-and-conquer might not be the most efficient approach compared to iterative or dynamic programming methods. The choice of strategy depends on the specific problem and context.

5. Difficulty in Implementation: Implementing divide-and-conquer algorithms can be more challenging, especially for beginners. The recursive nature and merging steps require careful design to ensure correctness and efficiency.

6. Stack Overflow Risk: Deep recursion can lead to stack overflow errors if the recursion depth exceeds the system’s stack capacity, particularly with large inputs or poorly designed algorithms.

Conclusion

The Divide and Conquer method is a cornerstone of algorithm design. It allows for the efficient solution of complex problems by breaking them down into simpler sub-problems, solving each one independently, and then combining the results. Understanding this paradigm is crucial for tackling a wide range of computational problems effectively.

Python code for Merge Sort- Divide and conquer method

def merge_sort(arr):

    # Base case: if the array has 1 or 0 elements, it is already sorted

    if len(arr) > 1:

        # Divide the array into two halves

        mid = len(arr) // 2  # Find the middle of the array

        left_half = arr[:mid]  # Left sub-array

        right_half = arr[mid:]  # Right sub-array

        # Conquer: Recursively apply merge_sort to both halves

        merge_sort(left_half)

        merge_sort(right_half)

        # Combine: Merge the two halves

        i = j = k = 0

        # Merge data from left_half and right_half into the original array

        while i < len(left_half) and j < len(right_half):

            if left_half[i] < right_half[j]:

                arr[k] = left_half[i]

                i += 1

            else:

                arr[k] = right_half[j]

                j += 1

            k += 1

        # Check if any elements were left in left_half

        while i < len(left_half):

            arr[k] = left_half[i]

            i += 1

            k += 1

        # Check if any elements were left in right_half

        while j < len(right_half):

            arr[k] = right_half[j]

            j += 1

            k += 1

# Example usage:

arr = [11, 6, 3, 24, 46, 22, 7]

print("Original array:", arr)

merge_sort(arr)

print("Sorted array:", arr)

Output

Original array: [11, 6, 3, 24, 46, 22, 7]

Sorted array: [3, 6, 7, 11, 22, 24, 46]

Finding the Maximum Element in an Array

Given an array of integers, find the maximum value in the array.

Step-by-Step Solution

1. Initial Setup:

Begin with the entire array and determine the range to process. Initially, this range includes the entire array from the first element to the last element.

2.Divide

If the array contains more than one element, split it into two approximately equal halves. This splitting continues recursively until each subarray has only one element.

3. Conquer:

• For subarrays with only one element, that element is trivially the maximum for that subarray.

• For larger subarrays, recursively apply the same process to each half of the subarray.

4. Combine:

After finding the maximum element in each of the smaller subarrays, combine the results by comparing the maximum values from each half. Return the largest of these values as the maximum for the original array.

Python Implementation

def find_max(arr, left, right):

    # Base case: If the array segment has only one element

    if left == right:

        return arr[left]

    # Divide: Find the middle point of the current segment

    mid = (left + right) // 2

    """ Conquer: Recursively find the maximum in the left and

    right halves """

    # Maximum in the left half

    max_left = find_max(arr, left, mid)

    # Maximum in the right half

    max_right = find_max(arr, mid + 1, right)

    # Combine: Return the maximum of the two halves

    return max(max_left, max_right)

# Example usage

array = [3, 6, 2, 8, 7, 5, 1]

result = find_max(array, 0, len(array) - 1)

print("Maximum element:", result)

# Output: Maximum element: 8

Example: ( University Question)

you are working as a financial analyst for a bank.the bank has received a list of loan interest rates from multiple branches, and you need to identify the two lowest rates to recommend the most cost-effective options to customers. The rates are provided as an array of positive integers and your task is to develop an efficient algorithm using the divide and conquer approach to find the sum of the two smallest rates/ explain with suitable example

To solve the problem using a divide and conquer approach, we can break the problem into smaller sub problems, solve them, and combine the results to find the two smallest loan interest rates efficiently.

---

Algorithm

Steps:

1. Divide the Array:

   • Split the array into two halves until each subarray contains only one or two elements.

2. Conquer (Find Two Smallest in Each Subarray):

   • For each subarray, determine the two smallest numbers directly if the size is $\leq 2$.
   • Otherwise, recursively solve for the two smallest numbers in each half.

3. Combine the Results:

   • Merge the results from the two halves by selecting the two smallest numbers among the four candidates (two from each half).

4. Return the Sum:

• Add the two smallest numbers obtained.

Explanation with Example

Input:

arr = [5, 2, 8, 6, 3, 1]

Steps:

1. Divide the Array:

   • Split the array recursively until each subarray has 1 or 2 elements:

     
     [5, 2, 8, 6, 3, 1]
     -> [5, 2, 8] and [6, 3, 1]
     -> [5, 2] and [8] for the first half; [6, 3] and [1] for the second half.
     

2. Conquer:

   • Find two smallest numbers in each subarray:

     
     [5, 2] -> (2, 5)
     [8] -> (8, ∞)
     [6, 3] -> (3, 6)
     [1] -> (1, ∞)
     

3. Combine Results:

   • Merge the results:

     
     First half ([2, 5], [8, ∞]) -> [2, 5, 8, ∞] -> (2, 5)
     Second half ([3, 6], [1, ∞]) -> [3, 6, 1, ∞] -> (1, 3)
     

   • Combine the two halves:

     
     [2, 5] and [1, 3] -> [2, 5, 1, 3] -> (1, 2)
     

4. Result:

   • Smallest: $1$
     
   • Second Smallest: $2$
     
   • Sum: $1 + 2 = 3$
     

Output:

Sum of two smallest rates: 3

Python Implementation

def find_two_smallest(arr):

    # Base case: If the array has only one element, return the element and infinity

    if len(arr) == 1:

        return arr[0], float('inf')

    # Base case: If the array has two elements, return the smallest and the second smallest

    if len(arr) == 2:

        return (min(arr[0], arr[1]), max(arr[0], arr[1]))

    # Divide the array into two halves

    mid = len(arr) // 2

    left_smallest, left_second = find_two_smallest(arr[:mid])

    right_smallest, right_second = find_two_smallest(arr[mid:])

    # Combine results from the two halves

    candidates = [left_smallest, left_second, right_smallest, right_second]

    candidates.sort()  # Sort to find the two smallest numbers

    return candidates[0], candidates[1]  # Return the two smallest numbers

def sum_two_smallest(arr):

    smallest, second_smallest = find_two_smallest(arr)

    return smallest + second_smallest

# Example Usage

rates = [5, 2, 8, 6, 3, 1]

result = sum_two_smallest(rates)

print("Sum of the two smallest rates:", result)

Output:

Sum of the two smallest rates: 3