Randomized Algorithms

Randomized approaches are powerful problem-solving techniques that leverage randomness to simplify complex problems or explore large solution spaces efficiently. These approaches are especially useful when deterministic algorithms may be too slow or difficult to implement.

For example consider  the ”random walk on a grid”, where a person starts at a fixed point on a grid and takes steps in random directions. The goal is to determine the expected time it takes for the person to return to the starting point. Simulating this random walk multiple times allows us to estimate the average return time, offering insights into the behavior of random processes.

Another example is the ”random coin flips” problem, where we want to determine the probability of getting a certain number of heads in a series of coin flips. For instance, simulating 100 coin flips repeatedly and counting the number of heads in each simulation allows us to estimate the probability distribution of getting a specific number of heads. This example highlights how simulations can be used to analyze probabilistic events and gain empirical insights into the behavior of random processes

Motivation for the Randomized Approach

The randomized approach to problem-solving offers several compelling advantages that can make it a valuable tool in both theoretical and practical applications.

Some of them are as follows:

• Complexity Reduction: A randomized approach often simplifies complex problems by introducing probabilistic choices that lead to efficient solutions.
• Versatility: Applicable across diverse domains, from combinatorial optimization to stochastic simulations, where deterministic solutions may be impractical or infeasible
• Performance: In certain scenarios, a randomized approach can offer significant performance improvements over deterministic counterparts, particularly when dealing with large datasets or complex systems

Key Features of Randomized Approaches:

1. Randomness as a Tool: Unlike deterministic algorithms, which follow a specific sequence of steps, randomized algorithms use random numbers or random decisions during execution. This helps in reducing time complexity or avoiding pitfalls like local optima.

2. Probabilistic Guarantees: Since randomness is involved, the results may not be the same on every run. However, with enough trials, these algorithms can provide answers that are correct with a high probability or give approximate solutions that are close to optimal.

3. Types of Randomized Algorithms:

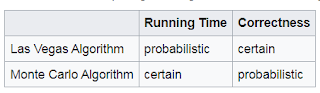
   • Las Vegas Algorithms: These algorithms always give the correct result, but their runtime may vary depending on the random choices made. An example is randomized quicksort, where the pivot is selected randomly to avoid worst-case scenarios.
   • Monte Carlo Algorithms: These algorithms might give incorrect results with some probability but are faster in execution. For example, Monte Carlo methods are often used in numerical simulations where an exact solution is hard to compute.

1. Advantages:

• Simplicity: Randomized approaches can simplify the design of algorithms, making them easier to implement.
• Efficiency: In some cases, randomized algorithms are faster than their deterministic counterparts because they avoid worst-case scenarios that are unlikely to occur randomly.
• Parallelization: Randomized algorithms are often easy to parallelize, making them suitable for large-scale problems in areas like machine learning, cryptography, and computational biology.

Randomized Approach Vs Deterministic Method:

Randomized approaches and deterministic methods each offer unique advantages and are suited to different types of problems. Randomized methods incorporate elements of chance, which can simplify complex issues and provide efficient solutions when dealing with large or variable datasets. For example,consider a company that wants to estimate customer satisfaction levels across a vast number of branches. Instead of surveying every customer at each branch, the company could randomly select a few branches and survey a sample of customers from those locations. This approach provides a statistically valid estimate of overall satisfaction while avoiding the need for exhaustive data collection.

In contrast, deterministic methods are based on predictable, fixed processes and deliver consistent results each time they are applied. For instance, if you need to calculate the total cost of items in a shopping cart, you would use a deterministic approach where each item’s price is added together to get an exact total. This method ensures accuracy and repeatability but may be less adaptable when dealing with uncertainty or incomplete data, such as predicting future sales based on historical trends.

Randomized approaches are especially beneficial in scenarios where processing or analyzing every possible option is impractical. For instance, if a researcher wants to estimate the average time people spend exercising each week, they might use randomized surveys to gather data from a representative sample of individuals rather than interviewing everyone. This method allows for efficient data collection and analysis, offering insights into exercise habits without the need for comprehensive surveys of every individual.

On the other hand, deterministic methods are ideal for situations where precision and reliability are essential. For example, when designing a new piece of machinery, engineers use deterministic methods to perform precise calculations to ensure the machinery operates safely and efficiently. These methods provide exact and consistent results, which are crucial for meeting stringent safety and performance standards. The choice between randomized and deterministic methods depends on the nature of the problem, including the need for accuracy, efficiency, and the ability to handle variability and uncertainty. 

In essence, randomized approaches give us flexibility and efficiency, particularly in cases where deterministic methods might be less practical.

Solving Computational Problems Using Randomization

Let us look at how to solve computational problems using randomization. To get an idea of how to solve computational problems using randomization, let us start with the problem of estimating the value of Pi (π).A common randomized approach to estimate the value of Pi (π) is the Monte Carlo method. This method involves simulating random points in a square that contains a quarter circle and calculating the ratio of points that fall inside the quarter circle to the total number of points.

Monte Carlo Method to Estimate π

1. Generate random points within a unit square (1 × 1).

2. Count how many points fall inside a quarter circle of radius 1.

3. The ratio of points inside the quarter circle to the total points approximates

the area of the quarter circle ( π/4 ).

4. Multiply this ratio by 4 to estimate π.

Here is a Python code to estimate π using the Monte Carlo method:

import random

num_samples = 1000000 # Number of random points to generate

inside_circle = 0 # points inside unit circle

for _ in range(num_samples):

        x = random.random()

        y = random.random()

        if x**2 + y**2 <= 1:

            inside_circle += 1 #increment count if the point is inside circle

pi_estimate = (inside_circle / num_samples) * 4

print(f"Estimated value of pi with {num_samples} samples:{pi_estimate}")

Output:

Estimated value of pi with 1000000 samples:3.14306