Algorithmic Thinking with Python KTU BTech S1 UCEST 105 2024 scheme - Dr Binu V P

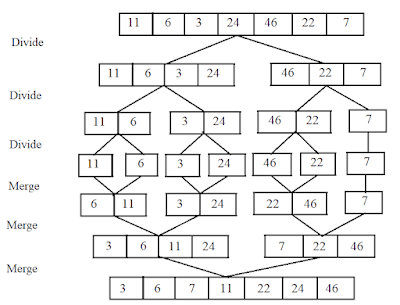
  Recursion vs Dynamic Programming Aspect Recursion Dynamic Programming (DP) Basic Idea Solves a problem by breaking it down into smaller sub-problems, often leading to repeated calculations of the same sub-problems. Solves a problem by breaking it down into smaller sub-problems, but stores the results of these sub-problems to avoid redundant calculations. Overlapping Sub-Problems Sub-problems are often recalculated multiple times because results are not stored. Sub-problems are solved once and their results are stored (usually in a table) for reuse. Optimal Substructure Can be used if the problem exhibits optimal substructure, but does not explicitly take advantage of it unless combined with memoization. Explicitly takes advantage of optimal substructure by building up the solution from the smallest sub-problems. Time Complexity Can be exponential in many cases (e.g., O(2^n) for Fibonacci) due to repeated calculations. Often reduces time complexity to polynomial (e.g., O(n) for Fi...

Imagine you need to travel by taxi from Thiruvananthapuram to Ernakulam.You have several possible routes through different cities, and your goal is to find the one that gets you to Ernakulam in the shortest time, which you call the optimal route. Your cousin in Alappuzha knows the best route from Alappuzha  to Ernakulam. Given that any optimal route from Thiruvananthapuram must pass through Alappuzha, you can simplify your task by first finding the best route from Thiruvananthapuram to Alappuzha, which is closer and has fewer possible routes. Once you have this route, you can follow the one your cousin has suggested from Alappuzha to Ernakulam. This approach is based on the principle of optimality, which states that any optimal route from Thiruvananthapuram to Ernakulam via Alappuzha must have optimal sub-routes. Specifically, the segment from Alappuzha to Ernakulam must be the best route between these two cities, and the segment from Thiruvananthapuram to Alappuzha must also be op...

Imagine a classroom scenario where students are asked to organize a large number of books in a library. The problem of categorizing and shelving thousands of books can seem difficult at first. By applying divide-and-conquer principles, the task can be simplified significantly.The students can start by dividing the books into smaller groups based on genres, such as fiction, non-fiction, and reference. Each genre can then be further subdivided into categories like science fiction, historical novels,and biographies. Finally, within each category, the books can be organized alphabetically by author. This method of dividing the problem into manageable parts, solving each part, and then combining the results effectively demonstrates how divide-and-conquer can make complex tasks more approachable In software development, the divide-and-conquer approach is frequently employed in designing complex systems and applications. For instance, consider developing a comprehensive e-commerce platform. T...

The greedy method is a popular problem-solving approach used in algorithms where we make a series of choices, each of which looks best at the moment, with the hope of finding an optimal solution. What is the Greedy Method? In simple terms,   the greedy method   solves a problem by making the   locally optimal choice   at each step, with the hope that these local choices lead to a globally optimal solution. Here’s a breakdown of how this works: Make a decision   that seems best at the moment. Move to the next step and make another locally optimal choice. Repeat this process until the problem is solved. The main idea is that   you never reconsider decisions   once they are made, which makes this approach very efficient in terms of time. However, this also means that the greedy method may not always lead to the best overall solution for every problem—just the best you can get based on the choices made along the way. Key Characteristics of the Greedy Metho...

Password guessing using the brute force method involves systematically trying every possible combination of characters until the correct password is found. This approach is similar to padlock brute forcing, but it's applied to digital passwords instead of physical locks. Steps in Brute Force Password Guessing: Understanding the Password Structure : Character Set : Determine the possible characters in the password (e.g., lowercase letters, uppercase letters, numbers, special characters). Password Length : Consider the possible length of the password. If the length is unknown, you may need to start with shorter lengths and gradually increase. Systematic Trial : Starting Point : Begin with the shortest possible password, using the first character in the character set (e.g.,  a  if the set is just lowercase letters). Incrementing Combinations : Progress through each possible combination by adding characters from the set. For example: If the character set is  a-z , and the pas...

  Motivations for the Greedy Approach The greedy approach is a problem-solving technique that builds up a solution by choosing the best option available at each step, with the hope that these local choices will lead to an optimal global solution. It is often used in optimization problems where we aim to maximize or minimize some value. Let's explore why we consider this approach: Simplicity and Efficiency The greedy approach is intuitive and easy to implement because it breaks down a complex problem into smaller, manageable steps. Instead of backtracking or exploring multiple solutions, the algorithm selects the best option at each step, which simplifies the problem-solving process. Locally Optimal Choices At each decision point, the algorithm picks what seems to be the best choice, also known as the "locally optimal" solution. The assumption here is that these local choices will accumulate into a globally optimal solution. Although this doesn't always guarantee an o...

The greedy algorithm is a problem-solving approach that builds up a solution step by step by choosing the most immediate, locally optimal choice at each step, with the hope of finding a globally optimal solution. This method is widely used for optimization problems where you aim to maximize or minimize some value, like profit, cost, or time. Let’s discuss the characteristics of greedy algorithms in detail, so you can better understand when and why this strategy works. Characteristics of Greedy Algorithms: 1. Greedy Choice Property This is the core principle of any greedy algorithm. The greedy choice property states that a solution can be constructed by making a sequence of choices, where each choice is the best available at that moment (locally optimal). Once a choice is made, it is never reconsidered. What it means : At every step of the algorithm, you make a choice that looks the best without worrying about the future. 2. Optimal Substructure For a problem to be solved using a gree...